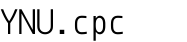投稿者 NOSS | 2019-05-10
こんにちは、NOSSです。今日はC++講習会第2回目とバーチャルコンテストを行いました。
C++講習会
APG4bの「1.08.変数のスコープ」から「1.12.文字列と文字」までと配列について説明を行いました。
C++の基本についてはほぼ完了したので後はAtCoder Problemsで問題を解いていくと強くなれると思います。
入部関係の話
現部員含めて今年度の部員名簿に記名してもらいました。5月中の活動で受け付けています。
5月18日(土)に新歓食事会を予定しています。参加したい方はTwitterのDMなどでも連絡をください。期限は5/13(月)までです。
コンテストの解説
コンテストのリンクはこちら
ABC008 A - アルバム
https://atcoder.jp/contests/abc008/tasks/abc008_1
$T-S+1$ が答えです。
ARC002 A - うるう年
https://atcoder.jp/contests/arc002/tasks/arc002_1
if文で場合分けをします。コード例を参考にして下さい。
ABC006 A - Shiritori
https://atcoder.jp/contests/abc060/tasks/abc060_a
文字列 $S$ の先頭は $S[0]$、末尾は $S[S.size()-1]$ でアクセスできます。
ABC115 B - Christmas Eve Eve
https://atcoder.jp/contests/abc115/tasks/abc115_b
もっとも値段の高い品物を半額にしてもらうのが最適なので答えは $\sum p_i - p_{max} / 2$ となります。
ABC073 C - Sentou
https://atcoder.jp/contests/arc073/tasks/arc073_a
$i$ 人目がスイッチを押してから、 $i+1$ 人目が来るまでのことを考えてみます。
-
$t_{i+1} - t_i \le T$ のとき
この間、お湯は流れ続けます。 -
$t_{i+1} - t_i \gt T$ のとき
$T$ 秒間お湯が流れてから止まります。
以上より、$i$ 人目と $i+1$ 人目の間のお湯が流れる時間がわかりました。
よって、各人について次の人が来るまでの時間を求め、$\min(T, t_{i+1} - t_i)$ の総和を求めれば答えとなります。
$N$ 人目の後には誰も来ないことに注意してください。
ABC078 D - ABS
https://atcoder.jp/contests/abc078/tasks/arc085_b
まず、$N=1$ のとき答えは $|a_1 - W|$ です。
$N \ge 2$ のときを考えます。先手は初手で $N$ 枚すべて取ることによって $|a_N - W|$ にすることができます。
また、初手で $N-1$ 枚取ることによって $|a_{N-1} - a_N|$ にすることができます。
初手で $k$ 枚取ったときを考えます($1 \le k \le N-2$)。 このとき後手は $N-1$ 枚目を取ることによっていつでもスコアを $|a_{N-1} - a_N|$ にすることができます。 つまり、今後スコアが大きくなってしまうパターンがあったとしても $N-1$ 枚目をとれば $|a_{N-1} - a_N|$ にできるのでスコアは少なくとも $|a_{N-1} - a_N|$ 以下にすることができます。
先手の手番についても同様に、スコアが $|a_{N-1} - a_N|$ より小さくなってしまうパターンがあるならば $N-1$ 枚目をとって $|a_{N-1} - a_N|$ にすればいいので、少なくとも $|a_{N-1} - a_N|$ 以上にすることができます。
よって、互いに最善を尽くすとスコアは $|a_{N-1} - a_N|$ になることが分かります。
以上より、$N \ge 2$ のときゲームの結果は $|a_N - W|$ と $|a_{N-1} - a_N|$ の $2$ パターンしかないことが分かるので、$\max(|a_N - W|, |a_{N-1} - a_N|)$ が答えになります。
ARC021 C - 増築王高橋君
https://atcoder.jp/contests/arc021/tasks/arc021_3
部分点解法
毎回 $N$ 個の建物のうちコストが最小の建物を増築するのが最適です。
よって、$K$ 回のうち各回 $N$ 個の建物を愚直に調べれば $O(NK)$、優先度付きキューを使えば $O(K \log N)$ で答えが求まります。
満点解法
$K \le 10^{8}$ のため各回調べる方法はTLEになります。
ここで、増築がコストが小さい順に行われていくことに注目します。 $K$ 回目の増築にかかったコストを $X$ と置くと、$i$ 回目($1 \le i \le K$) の増築コストは $X$ 以下であることが分かります。
すなわち、各建物について増築コストが $X$ 以下である間は増築を続けていいことが分かります。
よって、ある $X$ を決め打つと各建物の増築可能な回数が求められます。$N$ 個の建物の増築可能回数の総和が $K$ 以上であれば、コスト $X$ 以下で $K$ 回の増築が行えることが分かります。
以上より、可能な $X$ の最小値を二分探索することで答えを得ることができます。
$X$ を求めたら
$(X未満のコストの総和) + X \times (K - (X未満でできる増築回数))$
を計算すればよいです。
計算量は $O(N \log X_{max})$ となります。
ARC028 C - 高橋王国の分割統治
https://atcoder.jp/contests/arc028/tasks/arc028_3
適当な根付き木を考えます。まず、葉は $N-1$ であることが分かります。 次に $1$ つ親の頂点をみると $i$個目の子の部分木を大きさを $s_i$ と置いて $\max( \max(s_i), N-1-\sum s_i)$ が答えであると分かります。
以上より、再帰的に答えを求めることができます。
計算量は $O(N)$ です。
ARC026 C - 蛍光灯
https://atcoder.jp/contests/arc026/tasks/arc026_3
DPで解を得ることができます。遷移に工夫が必要です。
$dp[i] =$ ちょうど $i$ メートル以内を照らすために必要な最小コスト
と置きます。遷移は
$$ dp[r[i]] = \min \left(dp[r[i]], \min_{l[i] \le j \le L} (dp[j] + c[i]) \right) $$
となります。蛍光灯は $l[i]$ が小さい順に調べます。
区間の最小値の取得にセグメント木を使用すれば $O(N \log L)$ 優先度付きキューなら $O(N \log N)$ で求められます。
あるいは以下のような有向グラフの最短経路問題としても解けます。